Les algorithmes évolutionnaires sont des solveurs universels qui sont adaptés à la résolution de problèmes difficiles, en particulier de problèmes multicritères rencontrés dans l’industrie.
Exemple :
Un exemple de problème difficile est celui dit du « voyageur de commerce » : un voyageur de commerce doit visiter un ensemble de villes et revenir à sa ville de départ. Les distances entre toutes les villes sont connues et son objectif est d’effectuer le parcours le plus court.
Pour ce problème, la recherche de la meilleure solution nécessite l’évaluation de tous les cas possibles.
En considérant 1 milliard de solutions (parcours possibles) testées par seconde, comparons les temps de calcul nécessaires pour 16 et 25 villes :
Pour 16 villes : 10 minutes
Pour 25 villes : 9.8 millions d’années !
On observe ici un phénomène d’explosion combinatoire avec l’augmentation de la taille du problème. On doit alors se résoudre, à partir d’un certain seuil, en fonction des ressources de calcul et du temps dont on dispose à abandonner la recherche de la solution optimale. On s’orientera alors vers la recherche d’une « bonne solution » dans un temps raisonnable. Un certain nombre d’algorithmes d’optimisation peuvent être mis en œuvre afin de traiter ce type de problème de cette façon comme par exemple : la méthode de Monte-Carlo, la méthode du « recuit simulé », les algorithmes évolutionnaires…
Les algorithmes d’évolution artificielle
Cet article s’intéresse aux algorithmes d’évolution artificielle.
Le principe de ces algorithmes est de simuler de manière simplifiée l’évolution des êtres vivants selon les théories de l’évolution.
Les mécanismes simulés par les algorithmes évolutionnaires sont ceux :
– de la sélection naturelle (les individus les mieux adaptés à leur environnement ont des capacités plus importantes de survie et de reproduction)
– de la reproduction : le génotype de l’enfant est construit par héritage du génotype des parents.
– de la modification spontanée d’un ou plusieurs caractères génétiques par mutation
Ce type d’algorithme nécessite :
- la représentation d’une solution sous forme numérique (vecteurs de réels, entiers, booléens…) correspondant à des valeurs associées à la réalité à représenter
- de pouvoir évaluer les solutions (valeurs associées à la solution)
La représentation de la solution est en quelque sorte le génotype artificiel d’un « individu-solution» et son évaluation correspond à la qualité de la solution.
Dans l’exemple du voyageur de commerce, la représentation de la solution pourra par exemple être une liste des villes ordonnées selon le parcours envisagé.
Voici le schéma général d’un algorithme évolutionnaire :
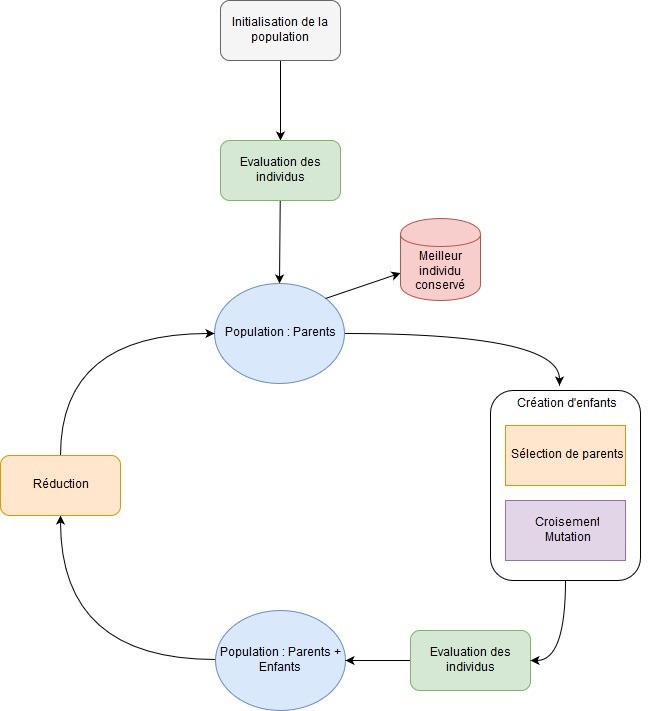
L’algorithme commence par l’initialisation d’une population de taille fixe dont les individus sont générés de manière aléatoire. Les individus sont ensuite évalués à l’aide d’une fonction d’évaluation dont le résultat est attribué à l’individu et qui traduit la qualité de la solution qu’il représente. Cette évaluation est nécessaire pour pouvoir par la suite comparer les individus entre eux et permettre de décider de conserver ou non tel ou tel individu plutôt qu’un autre.
On recherchera selon le type de problème à optimiser soit le minimum de cette fonction d’évaluation (comme dans le cas du voyageur de commerce), soit le maximum (type de problème avec recherche de gain).
La première population créée est identifiée comme la population des « Parents ».
L’algorithme consiste ensuite en une suite d’itérations (une itération correspond à la création d’une nouvelle génération d’individus).
La première étape consiste à « fabriquer » des enfants. Un enfant peut être créé à partir d’un ou plusieurs parents. Le choix d’un ou des parents est effectué par une méthode de sélection, par exemple une sélection par tournoi déterministe : un nombre N de parents est tiré aléatoirement et le meilleur au sens de sa fonction d’évaluation est conservé. Chaque tournoi sélectionne 1 parent et l’opération se répète jusqu’à l’obtention du nombre de parents nécessaires.
Puis un enfant est créé à partir des gènes du ou des parents. Des opérateurs de croisement et de mutation sont appliqués aux gènes des parents selon des probabilités déterminées afin de constituer le génotype d’un enfant.
Cette opération se répète jusqu’à l’obtention d’une taille de population d’enfants fixée. Ces nouveaux individus sont évalués par la fonction d’évaluation (la même que celle appliquée aux individus parents de la première génération)
La nouvelle population constituée des parents et des enfants est soumise à une réduction de taille pour retrouver la taille de la population de parents. La réduction est un processus de sélection (par tournoi par exemple) qui s’appuie sur la valeur des individus attribuée par la fonction d’évaluation.
Le cycle se poursuit jusqu’à la vérification d’une condition d’arrêt (par exemple l’atteinte du nombre de cycles prévu, par exemple 500 cycles).
A chaque nouvelle population de Parents et dès la première génération, on s’assure de conserver globalement le meilleur individu produit par l’algorithme et à la fin de l’exécution de l’algorithme on dispose de la meilleure solution trouvée. Dans l’exemple précédent du voyageur de commerce, on récupère ainsi le meilleur parcours trouvé par l’algorithme.
Spécificité de ces algorithmes
L’originalité de ces algorithmes est liée à leur capacité à gérer une population d’individus qui représente des solutions potentielles diversifiées (tout au moins au démarrage de l’algorithme). Ces individus peuvent échanger des informations au sein de la population afin de produire de nouvelles solutions. De nouvelles solutions peuvent aussi apparaître sans échange d’informations entre individus grâce au phénomène de mutation.
L’algorithme élimine progressivement les moins bonnes solutions selon un processus non déterministe à chaque génération en simulant une pression de sélection sur les « individus-solutions ». Le phénomène qui apparaît couramment au cours de l’évolution artificielle est la convergence plus ou moins rapide de la population : après un certain nombre de cycles les individus présents tendent à se ressembler du point de vue de leur qualité et de leur génotype.
Ainsi lorsqu’une population a convergé, il n’est plus utile de poursuivre l’exécution de l’algorithme. La recherche de nouvelles solutions implique de relancer l’algorithme.
Performances
Les algorithmes évolutionnaires ont des propriétés qui permettent de paralléliser une bonne partie des opérations qui sont nécessaires pour les faire fonctionner. Ce parallélisme peut être facilement mis en œuvre sur certaines cartes graphiques et permettent ainsi d’améliorer leurs temps de réponse.
Un autre type d’approche pour obtenir une amélioration des performances est de mettre en œuvre un parallélisme en îlots. L’algorithme tourne alors sur plusieurs machines en même temps et de manière indépendante tout en procédant à des échanges contrôlés d’«individus-solutions » entre les îlots.
Conclusion
Les algorithmes évolutionnaires peuvent faire mieux qu’une recherche aléatoire à condition de mettre au point une représentation de la solution adaptée à la résolution du problème d’optimisation posé, puis de tester et mettre au point leur paramétrage. Ceci nécessite une véritable expertise.
Une erreur parfois commise est de considérer qu’il s’agit de solutions en « boite noire » prêtes à l’emploi. Le plus souvent cette utilisation conduit à des déconvenues car il faut au contraire réaliser une adaptation au problème à traiter.
Les algorithmes évolutionnaires sont intéressants pour :
– des problèmes non résolus tels qu’ils peuvent se rencontrer dans l’industrie (problèmes d’ordonnancement avec contraintes, comme par exemple l’optimisation de l’utilisation de machines de production, d’optimisation financière : http://sciences-fictions/journals/displayArticlesnew.jsp?paperID=9963 ),
– pour les problèmes dynamiques (dont l’évaluation de la qualité des solutions est changeante au cours du temps, comme le problème du voyageur de commerce qui doit prendre en compte les changements en temps réel de nouvelles villes à visiter ou d’annulation)
– pour les problèmes multicritères (problèmes de planning à contraintes multiples par exemple).